Clase #5 20/06/2022

Sesión #5

--------------------------------------------------------------------------------------------------

Teorema fundamental del cálculo integral

Si f es continua en [a,b], entonces la función 

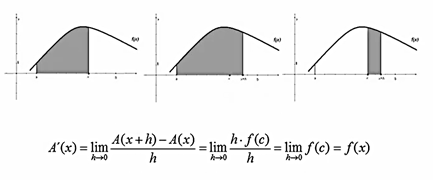
A(x)=Área bajo f entre a y x

Es una primitiva de f, es decir A´(x)=f(x) ya que 

Donde c es algún punto entre x y x+h

Regla de Barrow

La Regla de Barrow afirma que la integral definida de una función continua f(x) en el intervalo [a, b] es igual a la diferencia entre los valores que toma una función primitiva F(x) de f(x), en los extremos de dicho intervalo.

La regla se conoce como Regla de Barrow en honor a Isaac Barrow (1630-1677) y también como segundo teorema fundamental del cálculo.

Para resolver una integral definida de una función, es suficiente encontrar una primitiva de la función y sustituir en ella los límites superior e inferior de integración y restar ambos valores.

Las aplicaciones de la regla de Barrow son las aplicaciones de la propia integral definida. Esta regla se utiliza habitualmente para el cálculo de áreas encerradas entre la gráfica de funciones:

Integral indefinida

Definición:

Llamamos a f una integral indefinida de f en el intervalo, si:

dx=f(x), es decir, F´(x)=f(x)

La notación que emplearemos para referirnos a una antiderivada es la siguiente:

∫ f(x)dx=F(x)+C

Teorema:

Si F´(x)=G´(x), ∀xE(a,b), entonces existe una constante C tal que F(x)=G(x)+C, ∀xE(a,b)

---------------------------------------------------------------------------------------------------------------------------------------------------------------- 

Ejercicios trabajados en clase.

---------------------------------------------------------------------------------------------------------------------------------------------------------------- 

Bibliografía

Teorema fundamental del calculo. Superprof. (2020). Recuperado el 5 de Julio del 2022, de https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/teorema-fundamental-del-calculo-y-de-la-media.html.