Clase #3 10/06/2022
Sesión #3
---------------------------------------------------------------------------------------------------------------
En esta sesión se dio un repaso de la aplicación de
diferenciales en el cálculo de errores y entramos de lleno en el inicio del
cálculo integral.
Cálculo Integral
La integración es un concepto fundamental de las matemáticas
avanzadas, una integral puede ser definida como la suma de infinitos sumandos,
infinitamente pequeños.
De forma que el cálculo integral es la rama de las
matemáticas dedicada al proceso de integración, común en la ingeniería.
Una integral definida de una función representa el área
limitada por la gráfica de la función.
El origen del cálculo como tal se remonta a la época de Arquímedes,
los primeros en usarlo fueron figuras como Descartes, Newton y Leibniz.
Newton aportó de gran manera al cálculo integral con su
teorema fundamental, el cual dicta que la derivación y la integración son
procesos totalmente inversos.
La introducción del cálculo integral vino por parte de J.
Bernoulli, quien escribió el primer curso de cálculo integral en 1792, sin
embargo, el hombre que exploró el cálculo en toda su profundidad fue Euler,
quien es el responsable de que los métodos de integración indefinidas alcancen
su nivel actual.
Al resolver una integral obtenemos la denominada
"Antiderivada" o "Primitiva"
Teorema fundamental del cálculo
El teorema fundamental del cálculo dice que la derivada de
la integral {F(x)} de la función continua {f(x)} es la propia {f(x)}.
f'(x)=f(x)
Gracias a que la derivación y la integración son operaciones
inversas, al integrar una función continua y luego derivarla se recupera la
función original.
En el cálculo integral se emplean las diferenciales, de modo
que a la derivada de una función se le agrega el factor dx.
df(x)= f'(x)dx
Definición de una integral indefinida
En cálculo integral se puede enunciar el problema como:
"Dada la diferencial de una función, hallar la función..."
-La operación se indica con el símbolo: " ∫
"
Por lo tanto, se expresa: " ∫
f'(x)dx=f(x) "
El conjunto de todas las primitivas de la función f(x) es
conocida como la integral indefinida de f con respecto a x, la cual se expresa
como: "∫f(x)dx
Donde:
- ∫: Símbolo de integral.
- f(x): Integrando.
- dx: Variable de integración.
Integración
Al resolver la integral indefinida, obtenemos la
antiderivada de dicha función.
∫ f(x)dx= F(x)+c
Donde "c" es la constante de integración.
La aplicación de las integrales definidas es muy común en la
ingeniería y en la matemática en general. Se utiliza principalmente para el
cálculo de áreas y volúmenes de regiones y solidos de revolución.
Propiedades de la integral indefinida
- La integral del producto de una constante por una función es igual al producto de la constante por la integral de la función.
----------------------------------------------------------------------------------------------------------------------------------------------------------------
Figuras importantes nombradas
Arquímedes
Euler
----------------------------------------------------------------------------------------------------------------------------------------------------------------
Ejercicios trabajados en clase.
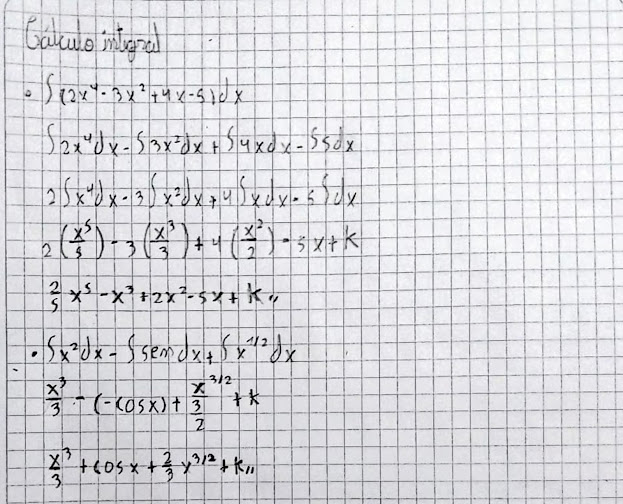
.png)











.jpeg)
.png)
.png)

Comentarios
Publicar un comentario