Clase #17 22/08/2022
Sesión #17
--------------------------------------------------------------------------------------------------
Volumenes de revolución
Si una función se gira con respecto a un eje del plano se genera un volumen conocido como sólido de revolución y al eje se le llama eje de revolución.
Un volumen del sólido de revolución se conforma de la suma infinita de franjas unitarias de volumen y si se genera haciendo girar a una función alrededor del eje se puede calcular por medio de.:
Donde a y b representan las rectas que lo limitan, es decir, son los extremos.
Mètodo del disco
Si giramos una región del plano alrededor de un eje obtenemos un sólido de revolución. El volumen de este disco de radio R y de anchura ω es:
Volumen del disco = R w
Para ver cómo usar el volumen del disco y para calcular el volumen de un sólido de revolución general, se hacen n particiones en la gráfica.
Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un disco es πR^2w, la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
Si se toma el eje de revolución verticalmente, se obtiene una fórmula similar:
----------------------------------------------------------------------------------------------------------------------------------------------------------------
Ejercicios trabajados en clase.
.png)
.png)

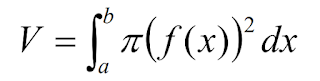

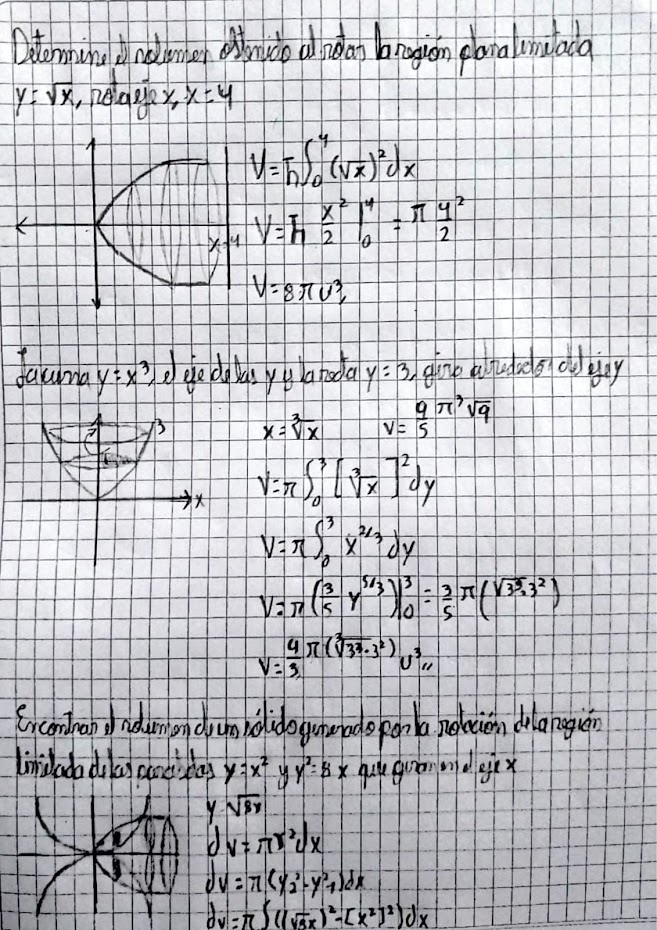
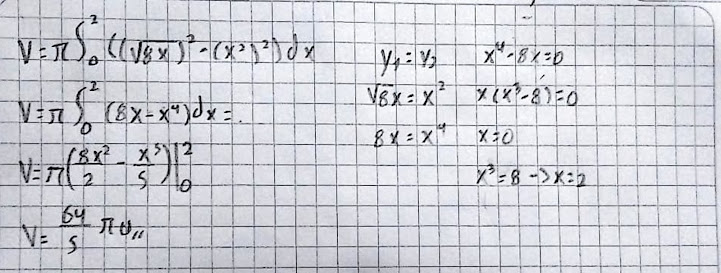
.png)
.png)

Comentarios
Publicar un comentario